Вероятность выпадения линий гексаграмм
при гадании по «Книге перемен»
Гадание по китайской «Книге перемен» заключается в построении и интерпретации гексаграмм, состоящих из шести линий.
䷾
Рис. 1. Пример гексаграммы
Линии, входящие в гексаграмму, могут быть сплошными или прерванными. Сплошная или прерванная линия, в свою очередь, может быть «молодой» (новой, актуальной) или «старой» (накануне изменения). В «Книге перемен» эти типы линий принято обозначать цифрами от шести до девяти:
| шестерка | - старая прерванная линия | --- --- * |
| семерка | - новая сплошная линия | -------- |
| восьмерка | - новая прерванная линия | --- --- |
| девятка | - старая сплошная линия | -------- * |
Тип линии определяется специальной процедурой, включающей деление пучка стеблей тысячелистника пополам с последующим пересчетом стеблей.
Процедура определения типа линий гексаграммы
От пучка из 50 стеблей отделяется один стебель и откладывается в сторону. В дальнейшем он не используется.
Первое изменение:
1. Пучок из 49 стеблей делят на две части: левую и правую.
2. Из правого пучка берётся один стебель и зажимается между мизинцем и безымянным пальцем левой руки.
3. Правой рукой из левого пучка отсчитывается по четыре стебля. Остаток – 1, 2, 3 или 4 стебля зажимаются между безымянным и средним пальцем левой руки.
4. Теперь отсчитывают по четыре стебля из правого пучка. Остаток – 3, 2, 1 или 4 стебля зажимают между средним и указательным пальцем.
После первого этапа в левой руке может оказаться 5 или 9 стеблей. Эти стебли откладывают в сторону, а остальные стебли собирают в пучок, в котором может быть 40 или 44 стебля. Для него выполняется второе изменение.
Второе изменение.
Повторяются действия 1 – 4. Между пальцами левой руки оказывается 4 или 8 стеблей. Стебли откладываются в сторону, остальные стебли собираются в пучок, в котором может быть 40, 36 или 32 стебля. Для него выполняется третье изменение.
Третье изменение.
Повторяются действия 1 – 4. Количество стеблей в руке и их комбинации те же, что и во втором изменении. Стебли откладываются в сторону, остальные стебли собираются в пучок, в котором может быть 24, 28, 32 или 36 стеблей.
От этого пучка отсчитывают по четыре стебля, получается 6, 7, 8 или 9 пучков, что соответствует полученному типу линии: «шестерке», «семерке», «восьмерке» или «девятке». Это число определяет первую (нижнюю) черту гексаграммы. Для получения всей гексаграммы описанные действия повторяют ещё пять раз.
Было показано*, что, при использовании данной процедуры, вероятность получения линий разного типа равна:
| шестерка | 1/16 |
| семерка | 5/16 |
| восьмерка | 7/16 |
| девятка | 3/16 |
* Смотрите, например, нашу статью «Построение гексаграмм Ицзин с помощью колоды игральных карт».
Однако, эти значения были рассчитаны для такого способа деления, при котором место деления пучка пополам располагается с равной вероятностью в любом месте пучка, как если бы при делении пучка из 49 стеблей, можно было бы с равной вероятностью получить 1 стебель, 24 стебля или 48 стеблей. Очевидно, что на практике место деления пучка пополам располагается не равновероятно по толщине пучка, а находится ближе к его середине. Также можно предположить, что точка деления пучка пополам отклоняется от его середины по закону нормального распределения. Поэтому возникают сомнения в том, что указанные выше вероятности справедливы на практике.
Для того, чтобы определить вероятность получения разных типов линий на практике, мы сделали следующее:
1. Собрали статистику деления пучка стеблей пополам и определили среднее значение и среднеквадратическое отклонение размера половинного пучка.
2. Провели компьютерное моделирование построения линий гексаграмм с использованием полученных статистических параметров и определили частоту получения разных типов линий.
Статистика деления пучка пополам
Для сбора статистики вместо стеблей тысячелистника использовались бамбуковые палочки диаметром 2,5 мм и длиной 21 см. Диаметр пучка из 50 таких палочек составляет около 2 см (для справки: диаметр пучка из настоящих стеблей тысячелистника составляет около 3 см).
Для деления использовался пучок из 44 палочек. Это число было выбрано потому, что в описанной выше процедуре сначала делится пучок из 49 палочек, затем пучки из 44, 40, 36 и 32 палочек, но вероятность получения пучков из 36 и 32 палочек относительно мала.
Для деления пучка пополам он захватывался ладонью левой руки, затем «на глаз» выбиралась его середина, и от этой середины большим и указательным пальцами правой руки отделялся правый пучок.
Было проведено 300 ручных делений пучка пополам. Собранная статистика, показана в Таблице 1 и на Рис. 2.
Таблица 1
| Размер пучка | Случаев |
| 14 | 2 |
| 15 | 5 |
| 16 | 19 |
| 17 | 31 |
| 18 | 40 |
| 20 | 40 |
| 21 | 49 |
| 22 | 34 |
| 23 | 33 |
| 24 | 20 |
| 25 | 16 |
| 26 | 9 |
| 27 | 2 |
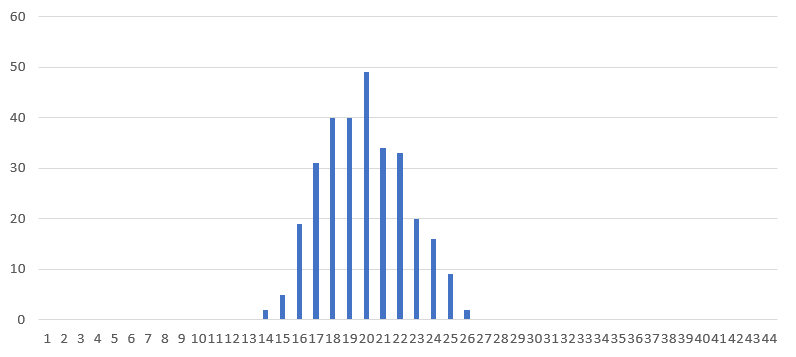
Рис. 2. Гистограмма распределения размера правого пучка
Параметры собранной статистики:
среднее значение, S – 19,85
среднеквадратическое отклонение, σ – 2,50
В полученных результатах интересно то, что среднее значение размера правого пучка 19,85 не равно 22, то есть, половине от 44. Это можно объяснить тем, что форма (сечение) пучка, захваченного левой рукой, не является симметричной (круг или эллипс), а больше напоминает яйцеобразную форму с узким концом, направленным к правой руке. Поэтому деление пучка по выбранной на глаз середине дает меньшее количество стеблей в правой части.
Компьютерное моделирование построения линий гексаграмм
Нами была написана программа для моделирования процесса построения линий гексаграмм на основе приведенной выше процедуры. При моделировании деления пучка пополам использовался генератор случайных чисел из библиотеки C++ std::mt19937. При делении пучков размером, отличающимся от 44, пропорционально изменялись среднее значение распределения и среднеквадратическое отклонение.
В следующей таблице приведены 10 результатов моделирования с 1000000 испытаний по построению линий линий гексаграмм для S = 19,85 и σ = 2,50. В таблице показаны частоты встречаемости «шестерок», «семерок», «восьмерок», «девяток» со значением для «шестерки», принятым за 1.
Таблица 2.
| № | Частоты линий |
| 1 | 1 / 5.22 / 7.17 / 3.11 |
| 2 | 1 / 5.14 / 7.11 / 3.08 |
| 3 | 1 / 5.15 / 7.12 / 3.08 |
| 4 | 1 / 5.16 / 7.10 / 3.08 |
| 5 | 1 / 5.15 / 7.11 / 3.08 |
| 6 | 1 / 5.19 / 7.16 / 3.09 |
| 7 | 1 / 5.16 / 7.13 / 3.08 |
| 8 | 1 / 5.16 / 7.12 / 3.07 |
| 9 | 1 / 5.14 / 7.10 / 3.06 |
| 10 | 1 / 5.17 / 7.15 / 3.08 |
Из таблицы видно, что полученные результаты незначительно отличаются от теоретических 1 / 5 / 7 / 3 рассчитанных для равномерного случайного деления пучка стеблей.
Нас также интересовало, как будут меняться результаты при изменении среднего значения середины пучка и среднеквадратического отклонения. С этой целью было проведено моделирование процесса построения линий для различных S и σ (1000000 испытаний для каждого варианта). Результаты представлены в Таблице 3.
Таблица 3
| S | σ = 4.0 | σ = 3.0 | σ = 2.0 | σ = 1.0 |
| 18 | 1 / 4.98 / 6.98 / 2.99 | 1 / 5.02 / 7.05 / 3.02 | 1 / 4.42 / 6.73 / 2.76 | 1 / 1.07 / 4.66 / 1.00 |
| 19 | 1 / 4.98 / 6.97 / 2.98 | 1 / 5.00 / 7.00 / 2.99 | 1 / 5.23 / 7.25 / 3.09 | 1 / 4.90 / 6.25 / 2.55 |
| 20 | 1 / 5.00 / 6.98 / 3.00 | 1 / 5.04 / 7.04 / 3.00 | 1 / 5.94 / 7.65 / 3.41 | 1 / 52.35 / 22.21 / 19.43 |
| 21 | 1 / 5.00 / 6.98 / 3.00 | 1 / 5.02 / 7.00 / 3.00 | 1 / 5.37 / 7.20 / 3.16 | 1 / 18.51 / 14.48 / 8.27 |
| 22 | 1 / 5.01 / 7.03 / 3.02 | 1 / 4.96 / 6.92 / 2.98 | 1 / 4.40 / 6.58 / 2.72 | 1 / 1.06 / 3.46 / 0.94 |
| 23 | 1 / 4.99 / 7.00 / 3.00 | 1 / 4.99 / 6.98 / 2.98 | 1 / 4.28 / 6.50 / 2.67 | 1 / 0.78 / 3.34 / 0.82 |
| 24 | 1 / 4.98 / 6.97 / 2.99 | 1 / 4.98 / 6.98 / 2.99 | 1 / 5.08 / 7.01 / 3.04 | 1 / 11.59 / 12.07 / 5.74 |
Из таблицы видно, что отклонение выбранной середины от реальной середины пучка (ошибка в выборе середины) мало влияет на частоты встречаемости линий разного типа. Эти частоты больше зависит от среднеквадратического отклонения. Если пучок делится пополам достаточно точно в одном и том же месте (σ < 2.0 – что соответствует отклонению всего в 1-2 стебля вправо или влево от одного места), то конечный результат теряет свою регулярность.
В. Загребельный, август, 2025 г.
Читайте также: В. Загребельный «Гадание по «Книге перемен»», 2025
| © Загребельный В.А., 2025 |